11pi 4 On Unit Circle

Tan 3pi/4

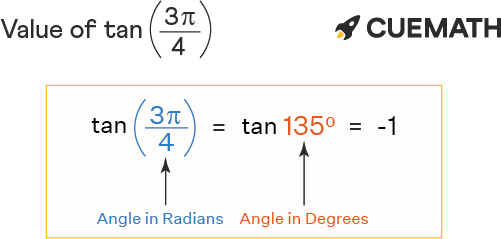
The value of tan 3pi/four is -i. Tan 3pi/4 radians in degrees is written every bit tan ((3π/4) × 180°/π), i.e., tan (135°). In this commodity, nosotros will discuss the methods to find the value of tan 3pi/4 with examples.

Tan 3pi/iv: -1
Tan (-3pi/4): 1
Tan 3pi/iv in degrees: tan (135°)

What is the Value of Tan 3pi/4?

The value of tan 3pi/iv is -1. Tan 3pi/4 can as well be expressed using the equivalent of the given bending (3pi/4) in degrees (135°).

Nosotros know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ 3pi/4 radians = 3pi/four × (180°/pi) = 135° or 135 degrees
∴ tan 3pi/4 = tan 3π/4 = tan(135°) = -1

Tan 3pi/4

Explanation:

For tan 3pi/4, the angle 3pi/4 lies between pi/two and pi (Second Quadrant). Since tangent function is negative in the second quadrant, thus tan 3pi/4 value = -1
Since the tangent office is a periodic part, nosotros can represent tan 3pi/four every bit, tan 3pi/4 = tan(3pi/4 + n × pi), northward ∈ Z.
⇒ tan 3pi/4 = tan 7pi/4 = tan 11pi/4 , and so on.
Note: Since, tangent is an odd role, the value of tan(-3pi/4) = -tan(3pi/4).

Methods to Detect Value of Tan 3pi/4

The tangent office is negative in the 2nd quadrant. The value of tan 3pi/four is given as -1. Nosotros can detect the value of tan 3pi/iv by:

Using Unit Circumvolve
Using Trigonometric Functions

Tan 3pi/four Using Unit of measurement Circumvolve

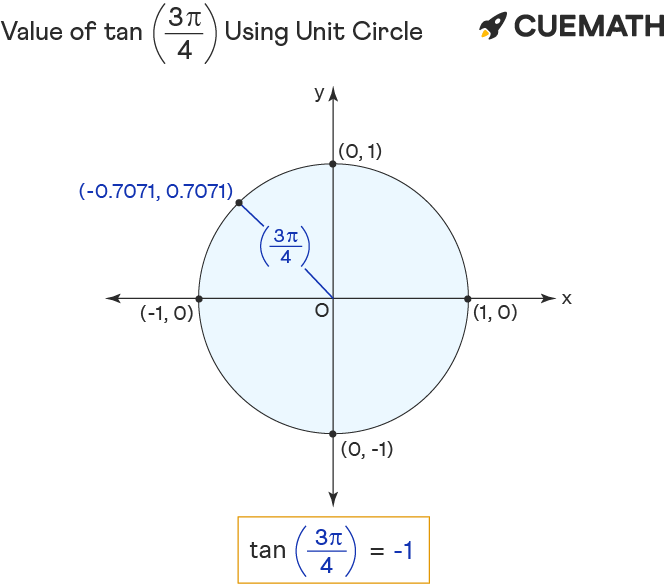
value of tan 3pi/4

To find the value of tan 3π/4 using the unit circle:

Rotate 'r' anticlockwise to form 3pi/4 angle with the positive x-centrality.
The tan of 3pi/4 equals the y-coordinate(0.7071) divided by the ten-coordinate(-0.7071) of the point of intersection (-0.7071, 0.7071) of unit circle and r.

Hence the value of tan 3pi/four = y/x = -one

Tan 3pi/4 in Terms of Trigonometric Functions

Using trigonometry formulas, we tin represent the tan 3pi/4 as:

sin(3pi/4)/cos(3pi/4)
± sin(3pi/4)/√(one - sin²(3pi/iv))
± √(1 - cos²(3pi/iv))/cos(3pi/iv)
± ane/√(cosec²(3pi/4) - one)
± √(sec²(3pi/4) - 1)
1/cot(3pi/4)

Note: Since 3pi/4 lies in the 2d Quadrant, the terminal value of tan 3pi/four will be negative.

We tin use trigonometric identities to stand for tan 3pi/iv as,

cot(pi/2 - 3pi/4) = cot(-pi/4)
-cot(pi/ii + 3pi/4) = -cot 5pi/4
-tan (pi - 3pi/4) = -tan pi/four

☛ As well Check:

sin 17pi/12
sin 4pi/3
sec pi
tan 11pi six
tan 19pi/3
sin 5pi/12

FAQs on Tan 3pi/4

What is Tan 3pi/4?

Tan 3pi/four is the value of tangent trigonometric function for an angle equal to 3π/4 radians. The value of tan 3pi/4 is -1.

How to Find Tan 3pi/four in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of tan 3pi/4 can be given in terms of other trigonometric functions as:

sin(3pi/iv)/cos(3pi/4)
± sin(3pi/iv)/√(1 - sin²(3pi/iv))
± √(1 - cos²(3pi/4))/cos(3pi/4)
± ane/√(cosec²(3pi/four) - 1)
± √(sec²(3pi/4) - 1)
1/cot(3pi/four)

☛ Likewise check: trigonometric table

What is the Value of Tan 3pi/4 in Terms of Cosec 3pi/4?

Since the tangent office tin exist represented using the cosecant function, we tin can write tan 3pi/4 as -1/√(cosec²(3pi/4) - 1). The value of cosec 3pi/four is equal to 1.41421.

What is the Value of Tan 3pi/4 in Terms of Sin 3pi/four?

Using trigonometric identities, nosotros can write tan 3pi/four in terms of sin 3pi/4 as, tan(3pi/4) = -sin(3pi/four)/√(1 - sin²(3pi/iv)) . Here, the value of sin 3pi/4 is equal to i/√2.

How to Find the Value of Tan 3pi/4?

The value of tan 3pi/4 can exist calculated by constructing an angle of 3π/4 radians with the x-axis, and and so finding the coordinates of the respective point (-0.7071, 0.7071) on the unit circle. The value of tan 3pi/4 is equal to the y-coordinate(0.7071) divided past the ten-coordinate (-0.7071). ∴ tan 3pi/four = -1